آزمون نرمال بودن

مطالب ارائه شده برگرفته از کتاب "راهنمای آسان تحلیل آماری با SPSS" تالیف آقای"رامین کریمی" است. کپی فقط با ذکر منبع مجاز می باشد.

پیش فرض های آماری، پایه بسیاری از آزمون های آماری تک متغیری و چندمتغیری است.شرایط مهم واساسی برای تحلیل داده های چندمتغیری، برقراری پیشفرض های نرمال بودن، خطّی بودن و یکسانی پراکندگی داده هاست. چنانچه یک یا چندتا از این مفروضه ها نادیده گرفته شود، در این صورت، در نتایج آماری سوگیری یا تحریف رخ می دهد (میزر و همکاران، 107:1391). قبل از انجام تحلیل های آماری تک متغیره و چندمتغیره (که پیش فرض های نرمال بودن، خطّی بودن، یکسانی پراکندگی و نبود هم خطّی چندگانه بین متغیرهای مستقل در مورد آنها باید صدق کند) باید برقراری پیش فرض های آماری را بیازماییم.
اگر انحراف از پیش فرض های آماری ناچیز باشد میتوان با کمی تسامح و تساهل این انحراف را نادیده گرفت و به ادامه تحلیل پرداخت. اگر انحراف از پیش فرض ها قابل توجه باشد باید یا از روش تبدیل داده ها برای برقرارکردن مجدد پیش فرض ها استفاده کنیم یا از آزمون های جایگزین استفاده کنیم که پیش فرض های فوق را مطرح نمی کنند (آزمون های ناپارامتریک).
در ادامه به توضیح چهار پیش فرض آماریِ نرمال بودن، خطّی بودن رابطه ها، یکسانی پراکندگی و نبود همخطّی چندگانه می پردازیم و روش آزمون هرکدام را توضیح می دهیم.

    آزمون نرمـال بودن داده ها
مفهوم توزیع نرمال در مورد داده های پارامتری صدق می کند (نه داده های ناپارامتری).آزمون نرمال بودن، با ایجاد یک نمودار احتمالِ نرمال بودن (به شکل زنگوله و نیز متقارن نسبت به میانگین)، به آزمون این فرض می پردازد که آیا مشاهدات پژوهش از توزیع نرمال تبعیت میکنند یا خیر. بسیاری از مشخصه های انسانی مانند هوش، نگرش ها و شخصیت در جمعیت (جامعه) دارای توزیع نسبتا نرمال هستند. البته توزیع نرمال به معنای توزیع استاندارد یا مطلوب نیست.
نرمال بودن، اساسی ترین پیش فرض تحلیل چندمتغیره است. اگر این فرض برقرار نباشد، برخی آزمون های آماری مشخص، غیرمعتبر بوده و قابل استفاده نیستند (هیر و دیگران،2010).اهمیت آشنایی و سنجش نرمال بودن توزیع داده ها در این است که برخی از روش های آماری مانند همبستگی پیرسون، آزمون های t و آزمون تحلیل واریانس بر فرض نرمال بودن توزیع داده ها (در جامعه) استوارند. همچنین برآورد پارامتر جمعیّت نیز با اتکاء به نرمال بودن توزیع متغیر در جمعیّت صورت می گیرد.

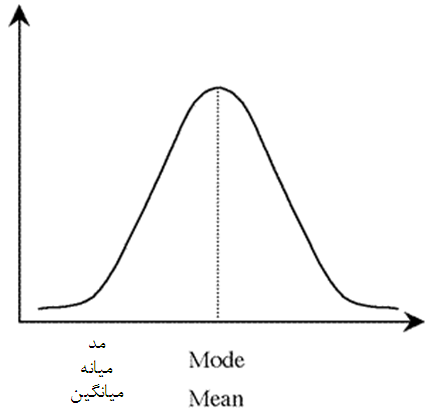
توزیع نرمال دارای ویژگی های زیر است:

     1. متقارن بوده، حداکثر ارتفاع در میانگین قرار دارد. نیمی از نمره ها در بالای میانگین و نیمی دیگر در پایین میانگین قرار دارد.

     2. مقادیر نما، میانه و میانگین برابر است.

      3.منحنی توزیع شبیه زنگوله است.

نکته: چنانچه توزیع یک متغیر در جمعیّت نرمال باشد و ما از این جمعیّت نمونه های با حجم 30 یا بیشتر (30≤n) به طور تصادفی ساده انتخاب کنیم، در این صورت توزیع متغیر در نمونه ما نیز نرمال خواهد بود.

برای تشخیص وضعیت توزیع داده ها (وضعیت نرمال بودن یا بررسی چولگی و کشیدگی) روش های متعددی وجود دارد. در جدول 3-2 برخی روش های تشخیص وضعیت نرمال بودن توزیع داده ها نشان داده شده است.

جدول 3-2- روش های عددی و تصویری ارزیابی وضعیت توزیع داده ها (آزمون های سنجش نرمال بودن)

انواع روش ها		ماهیت روش ها
روش های گرافیکی	روش های عددی	ماهیت روش ها
نمودار ساقه و برگ نمودار جعبه ای نمودار هیستوگرام	کشیدگی کجی	توصیفی
نمودار احتمال –احتمال (P-P) نمودار چارک –چارک (Q-Q)	آزمون کولموگروف-اسمیرنف آزمون شاپیرو - ویلک	مبتنی بر نظریه

(اقتباس از حبیب پور و صفری، 408:1388)

در این کتاب از بین روش های ذکر شده در جدول3-2، از روش های عددیِ کجی و کشیدگی و آزمون های کولموگروف- اسمیرنف و شاپیرو- ویلک بهره می گیریم.

1) کجی و کشیدگی

کجی یا چولگی در آمار، مقداری است از تقارن توزیع یک متغیر در اطراف میانگین. در واقع کجی، انحراف منحنی نرمال از حالت تقارن است. مقدار کجی می تواند مثبت یا منفی باشد. در حالت کجی مثبت، میانگین بزرگتر از میانه و میانه بزرگتر از مد است و در حالت کجی منفی، مد بزرگتر از میانه و میانه بزرگتر از میانگین است.
کشیدگی بیان کننده نحوه انباشته شدن نمره ها در مرکز توزیع یک متغیر است. در واقع کشیدگی، برآمدگی یا فرورفتگی منحنی توزیع نرمال است.در حالت کشیدگی تقارن توزیع حفظ می شود و دو نیمه منحنی متقارن هستند، اما نقطه اوج منحنی نرمال دچار تغییر می شود. مقدار کشیدگی می تواند مثبت یا منفی باشد. در حالت کشیدگی منفی، منحنی توزیع متغیر فررفته تر از حالت نرمال می شود و نقطه اوج توزیع متغیر، پایین تر از توزیع نرمال است. در حالت کشیدگی مثبت، منحنی توزیع متغیر برآمده تر از منحنی نرمال می شود و نقطه اوج توزیع متغیر، بالاتر از توزیع نرمال است.
در شکل شماره 3-5 منحنی توزیع نرمال و انواع حالت های کشیدگی و چولگی نمایش داده شده است.

برای مطالعه ادامه مبحث مطرح شده لطفا فایل زیر را دانلود کنید.

دانلود فایل PDF متن بالا