اجرای آزمون همبستگی پیرسون در SPSS
احتمالا، گسترده ترین کاربرد شاخص آماری همبستگی دو متغیری، ضریب همبستگی گشتاوری پیرسون است که به طور معمول همبستگی پیرسون نامیده میشود. علامت اختصاری آن rاست. ضریب پیرسون نشان می دهد که تا چه اندازه بین متغیرهای کمّی رابطه خطی وجود دارد(میزر، گامست و گارینو،152:1391).
کاربرد اصلیِ ضریب پیرسون زمانی است که متغیرها از نوع پارامتری باشند؛ بدین معنا که توزیع نرمال داشته باشند و در سطح فاصله ای/نسبی باشند. البته زمانی که متغیرها از نوع شبه فاصله ای باشند (یعنی هر متغیر ترکیبی از چند متغیر ترتیبی باشد که اصطلاحا به آن مقیاس های تراکمی میگویند)، برخی از پژوهشگران از ضریب پیرسون استفاده میکنند. برخی از نویسندگان استفاده از ضریب پیرسون برای یک متغیر دو ارزشی و یک متغیر فاصله ای/نسبی را هم مجاز شمرده اند. تفسیر همبستگی پیرسون زمانی که یکی از متغیرها دوارزشی (فقط شامل دو سطح) اما متغیر دیگر کمّی است نیز میتواند منطقی باشد(میزر، گامست و گارینو،164:1391).
تفسیر شدّت رابطه در همبستگی پیرسون
بعد از تعیین معنی داری و جهت رابطه، باید شدّت رابطه ارزیابی شود. برای تفسیر شدّت رابطه دومتغیر، تقسیم بندی های گوناگونی ارائه شده است. تقسیم بندی زیر یکی از آن هاست.
شیوه تفسیر شدت رابطه در همبستگی پیرسون
| شدّت رابطه |
تفسیر |
| 8/. تا 1 |
رابطه بسیار قوی |
| 6/. تا 8/. |
رابطه قوی |
| 4/. تا 6/. |
رابطه متوسط |
| 2/. تا 4/. |
رابطه کم (یا ضعیف) |
| صفر تا 2/. |
فقدان رابطه یا رابطه ناچیز |
(منبع: میلر، 299:1380)
مثال
در این بخش به بررسی همبستگی بین دو متغیر بهره هوشی و معدل مقطع کارشناسی می پردازیم. انتظار داریم که دو متغیر با یکدیگر همبسته باشند، به نحوی که با افزایش بهره هوشی، معدل افزایش بیابد. به عبارت دیگر انتظار داریم افرادی که بهره هوشی بالاتری دارند، معدل بالاتری هم داشته باشند. هر دو متغیر کمّی بوده و در سطح سنجش فاصله ای/نسبی قرار دارند. با توجه به این که هردو متغیر در سطح سنجش فاصله ای/نسبی هستند از همبستگی پیرسون استفاده میکنیم. از پیش فرض های آزمون همبستگی پیرسون نرمال بودن توزیع متغیر در جمعیّت آماری است، در این مثال فرض می کنیم که این پیشفرض برقرار است و توزیع داده ها نرمال است
اجـ ـرا
مسیر زیر را دنبال میکنیم:
Analyze--->Correlate--->Bivariate
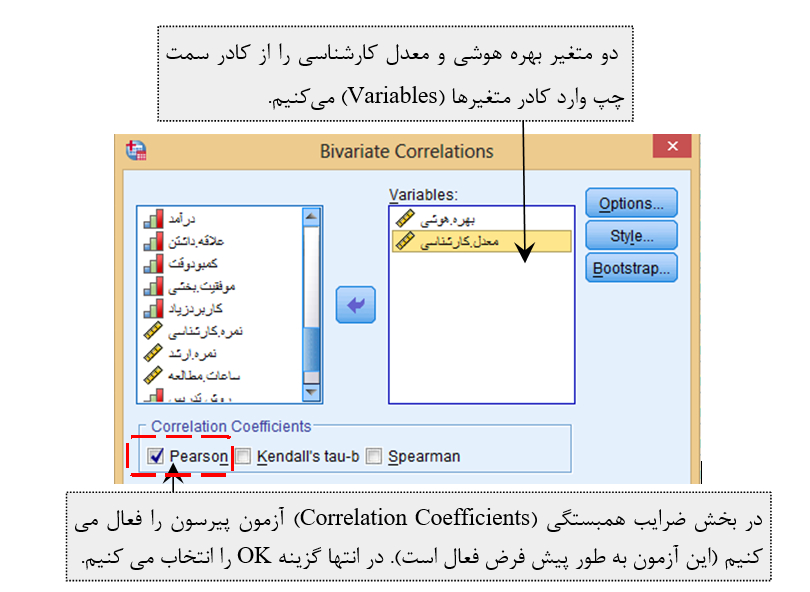
نتـ ـایج
در جدول بعد، نتایج آزمون همبستگی پیرسون بین دو متغیر بهره هوشی و معدل کارشناسی نشان داده شده است. نخست به سطح معنی داری به دست آمده نگاه میکنیم. سطح معنی داری به دست آمده برابر با 600/. به دست آمده است که بسیار بیشتر از مقدار مفروض 05/.است. در نتیجه بین دو متغیر بهره هوشی و معدل مقطع کارشناسی پاسخگویان رابطه معنی داری وجود ندارد. با توجه به این که بین دو متغیر همبستگی وجود ندارد، شدّت و جهت رابطه مورد بررسی قرار نمی گیرد.
| Correlations |
|
| |
بهره هوشی |
معدل کارشناسی |
| بهره هوشی |
Pearson Correlation |
1 |
-.053 |
| Sig. (2-tailed) |
|
.600 |
| N |
100 |
100 |
| معدل کارشناسی |
Pearson Correlation
همبستگی پیرسون |
-.053 |
1 |
| Sig. (2-tailed) |
.600 |
|
| N |
100 |
100 |
| |
|
|
|
|
گـ ـزارش:
در گزارش نتایج می نویسیم:
از آزمون همبستگی پیرسون جهت آزمون رابطه دو متغیر بهره هوشی و معدل مقطع کارشناسی استفاده شد. بین میزان بهره هوشی و معدل مقطع کارشناسی همبستگی معنی دار مشاهده نشد (600/. =P و 100=nو 053/.- = r). در نتیجه از جنبه آماری دو متغیر بهره هوشی و معدل کارشناسی با یکدیگر رابطه ندارند.
***
(فرض می کنیم رابطه به دست آمده معنی دار باشد و سطح معنی داری به دست آمده برابر با 004/. شده است و ضریب پیرسون برابر با 45/. به دست آمده است. در این صورت به این صورت گزارش می دهیم:
آزمون همبستگی پیرسون نشان داد که بین میزان بهره هوشی و معدل مقطع کارشناسی همبستگی وجود دارد (004/. =P و 100=nو 45/. = r). جهت رابطه بین بهره هوشی و معدل کارشناسی مثبت است. شدت همبستگی به دست آمده در حد متوسط است. واریانس توضیح داده شده 20.3% است. نتایج نشان می دهد دانشجویانی که بهره هوشی بالاتری دارند، معدل کارشناسی بالاتری هم کسب کرده اند.
چندنکته:
ضریب همبستگی پیرسون را با rنشان می دهند.
واریانس توضیح داده شده همان 2r است که از به توان دو رساندن ضریب همبستگی پیرسون (r) به دست می آید و نشان دهنده واریانس مشترک دو متغیر است.
بهتر است نمودار پراکندگی دو متغیر بهره هوشی و معدل در گزارش ذکر شود (قبل از نتایج آزمون همبستگی پیرسون).
کپی برداری تنها با ذکر منبع مجاز است
منبع: کتاب راهنمای آسان تحلیل آماری با SPSS؛ نویسنده: رامین کریمی