متغیر ها و داده های پرت در تحلیل نرم افزار spss

مطالب ارائه شده برگرفته از کتاب "راهنمای آسان تحلیل آماری با SPSS" تالیف آقای"رامین کریمی" است. کپی فقط با ذکر منبع مجاز می باشد.

داده های پِـرت

همیشه باید داده هایی (اطلاعاتی) که وارد برنامه هایی مانند اِکسل یا SPSS می کنیم را بررسی و بازبینی کنیم. همواره احتمال دارد که در داده ها با مقادیر غیرعادی مواجه شویم. موارد غیرعادی می تواند شامل مقادیر تعریف نشده و مقادیر پِرت (دور افتاده) باشد. همواره قبل از انجام هرگونه تحلیل آماری بر روی داده ها، باید چاره ای در مورد مقادیر پرت بیندیشیم.
افرادی که اندازه های انتهایی یا غیرمعمول در یک متغیر واحد (تک متغیری) یا در ترکیبی از متغیرها (چندمتغیری) دارند، دور افتاده یا پرت نامیده می شوند. داده های پرت اغلب سه یا بیش از سه واحد انحراف معیار (SD3±) از میانگین مربوط به خودشان فاصله دارند که از مشکلات احتمالی در ابزار اندازه گیری، شیوه ثبت یا ضبط پاسخ ها یا عضویت شرکت کنندگان در جامعه های که فرض می شود از آن نمونه گیری شده است، ناشی می شود. حضور داده های پرت می تواند نتایج تحلیل را به گونه های نامطلوب تحت تأثیر قرار دهد(تحریف کند). به همین دلیل بیشتر متخصصان پیشنهاد می کنند که اندازه های پرت قبل از تحلیل داده ها باید حذف شوند.

انواع داده های پرت
داده های پرت را می توان در دو دسته داده های پرت تک متغیری و داده های پرت چند متغیری تقسیم کرد:.
1) داده های پرت تک متغیری
داده های پرت تک متغیری مربوط به یک متغیر می شوند. به عنوان مثال وقتی که در یک پژوهش دانشجویی در زمینه میزان رضایت مردم از عملکرد شهرداری تهران؛ ما در متغیر سن افراد با عدد 150 روبرو می شویم!، به احتمال زیاد با داده پرت مواجه شده ایم. چرا که می دانیم احتمال وجود فردی با چنین سن و سالی بسیار بعید است! و یا وقتی که در متغیر درآمد، شخصی درآمد ماهانه خود را از یک کار تمام وقت 25 هزار تومان اعلام می کند و یا وقتی که در پاسخ سوالی که از فرد می پرسیم تا چه اندازه به آینده امیدوار است و او باید میزان رضایت خود را از عدد 1 (به معنای خیلی کم) تا عدد 5 (به معنی خیلی زیاد) اعلام کند، در فایل داده ها با عدد 6 روبرو می شویم (به دلیل اشتباه در ورود داده)، همگی نشان از وجود داده های پرت تک متغیری دارد که نخست باید آنها را شناسایی کرد و سپس در مورد آنها چاره ای اندیشید.
البته زمانی که با متغیرهای کیفی (اسمی و ترتیبی) سروکار داریم گاهی با مقادیری در داده ها روبرو می شویم که داده پرت محسوب نمی شوند اما مقادیری هستند که به اشتباه وارد شده اند و باید حذف شوند. مثلا در متغیر جنس، اگر ما زنان را با کد 1 و مردان را با کد 2 تعریف کرده باشیم و در این حال با عدد 1.5 در داده ها مواجه شویم؛ با داده پرت مواجه نیستیم اما با داده های اشتباه مواجه شده ایم (به دلیل اشتباه پاسخگو در پاسخ به سوال یا اشتباه در ورود داده) و باید آنها را شناسایی کرده و حذف یا اصلاح نماییم.

شناسایی داده های پرت تک متغیری
برای شناسایی داده های پرت تک متغیری باید از جدول فراوانی و نمودار جعبه ای استفاده کرد. از جدول فراوانی برای شناسایی داده های پرت در متغیرهای اسمی و ترتیبی استفاده می کنیم و از نمودار جعبه ای برای شناسایی داده های پرت در متغیرهای فاصله ای/نسبی. البته از جدول فراوانی هم می توان برای شناسایی داده های پرت در متغیرهای فاصله ای/نسبی استفاده کرد ولی نمودار جعبه ای برتری دارد و آسان تر است.

الف) جداول فراوانی
از جدول فراوانی برای کشف مقادیر پرت تک متغیری در متغیرهای اسمی و ترتیبی استفاده می کنیم. متغیرهایی مثل جنس، وضعیت تاهل، قومیت، تحصیلات و درآمد (هر دو به صورت چندگزینه ای و ترتیبی سنجیده شده باشند، مثلا تحصیلات در قالب سوالات دیپلم، فوق دیپلم، لیسانس و... سنجیده شده باشد) و یا تمام سوالاتی که در قالب طیف لیکرت سنجیده شده باشند. یعنی سوالاتی که پاسخ های آنان معمولا 3 تا 7 گزینه دارد و پاسخ هایی مثل کاملا موافقم تا کاملا مخالفم، اصلا تا همیشه و خیلی کم تا خیلی زیاد را در برمی گیرد. همچنین اگر متغیری فاصله ای/نسبی داشته باشیم که تعداد طبقات آن محدود (مثلا حدود 10 طبقه) باشد، می توانیم از جدول فراوانی استفاده کنیم.

مثال
در یک پژوهش (فرضی) از دانشجویان دختر و پسر دانشگاه شهید بهشتی خواسته شد تا میزان رضایت خودشان از عملکرد ریاست دانشگاه را اعلام کنند. بر این اساس از دانشجویان تعدادی سوال پرسیده شد که دو سوال آن عبارت بود از جنس دانشجویان و میزان رضایتشان از عملکرد ریاست دانشگاه. جنس دانشجویان شامل دو جنس (دختر کد 1، و پسر کد 2) و میزان رضایت در طیف لیکرت 5 گزینه ای (خیلی کم کد 1، کم کد 2 ، متوسط کد 3، زیاد کد 4 و خیلی زیاد کد 5) سنجیده شد. همانطور که مشاهده می شود ما هنگام ورود اطلاعات مربوط به جنس افراد به دانشجویان دختر کد یا عدد 1 و به دانشجویان پسر کد 2 داده ایم و در فایل داده ها و خروجی (برونداد) مربوط به آن، تنها باید عدد 1 و عدد 2 مشاهده کنیم. در مورد متغیر میزان رضایت هم تنها باید اعداد 1، 2، 3، 4 و 5 را مشاهده کنیم و نباید اعداد دیگری را (مثلا 6، 1.5، 20) مشاهده کنیم.

اجـ ـرا:
دستور فراوانی را اجرا می کنیم:

Analyze --->Descriptive Statistics --->Frequencies

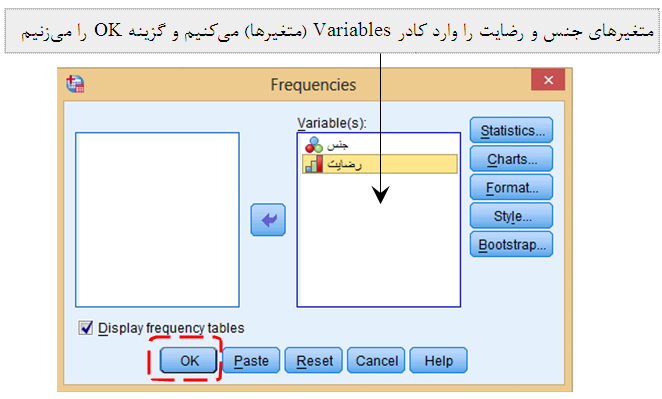
نتـ ـایج:
نتایج جدول فراوانی دو متغیر جنس و میزان رضایت در ادامه ارائه شده است. در جدول فراوانی جنس افراد مقادیر پرت مشاهده نمی شود، چرا که تنها دو کد یا طبقه 1 و 2 (دختر و پسر) وجود دارند. توجه شود که داده های گمشده (Missing) جزء داده های پرت به حساب نمی آیند. ما در فایل داده ها مقادیر گمشده را با عدد 9 نشان داده ایم و در فایل خروجی اعداد گمشده با عدد 9 ظاهر شده اند. به غیر از اعداد 1 و 2 و مقادیر گمشده، عدد دیگری در فایل خروجی جنس دانشجویان دیده نمی شود و بدین معناست که در متغیر جنس دانشجویان داده پرت وجود ندارد.
اما در متغیر میزان رضایت ما با اعدادی غیر از 1 ، 2، 3، 4 و 5 مواجه ایم و این اعداد مقادیر گمشده هم نیستند و نشان می دهد که دو مقدار پرت در داده ها وجود دارد (1.3 و 22) که باید در فایل داده ها شناسایی و حذف شود. چون پاسخگویان تنها می توانستند یکی از اعداد 1، 2، 3، 4 و 5 را انتخاب کنند در نتیجه اعداد دیگری که وجود دارند (1.3 و 22) مقادیر پرت حساب می شوند و باید از تحلیل حذف شوند.
لازم به ذکر است که عدد 1.3 داده پرت به حساب نمی آید و یک داده غیرعادی و تعریف نشده است. در اینجا به جهت آسان تر شدن آموزش، داده های غیرعادی و تعریف نشده در ارتباط با متغیرهای اسمی و ترتیبی را داده پرت به حساب آورده ایم.

برای مطالعه متن کامل این متن فایل زیر را دانلود نمایید.

دانلود فایل PDF متن کامل