مطالب ارائه شده برگرفته از کتاب "راهنمای آسان تحلیل آماری با SPSS" تالیف آقای"رامین کریمی" است. کپی فقط با ذکر منبع مجاز می باشد.

هـم­ خطّـی چـندگانه
هم ­خطّی حالتی است که در آن بین دو متغیر پیش­بین، همبستگی قوی وجود دارد. هم­ خطّی چندگانه حالتی است که در آن بیش از دو متغیر پیش بین همبستگی قوی با یکدیگر دارند. هم­ خطّی ­چندگانه می­ تواند تفسیر نتایج رگرسیون چندگانه را تحریف کند(میزر و دیگران،236:1391).
هم ­خطّی چندگانه زمانی اتفاق می­ افتد که متغیرهای مستقل چیز یکسانی را اندازه بگیرند. زمانی که دو یا چند متغیر مستقل همبستگی بالایی داشته باشند امکان وجود "­هم­ خطّی چندگانه" زیاد است. در ارتباط با گویه های یک متغیر نیز مساله هم ­خطی چندگانه وجود دارد. گویه­ هایی که مفهوم یکسانی را اندازه می­ گیرند باید با یکدیگر همبستگی بالایی داشته باشند، اما همبستگی­ های بزرگتر از 0/9 بین هرگویه می­ تواند موجب مشکلات آماری شود (تاباچینک و فیدل، 2001).
وقتی که هدف پژوهش تنها بیشینه کردن ضریب تعیین (R²) نیست، بلکه فهم تأثیر متقابل متغیرهای پیش­بین است، هم ­خطّی چندگانه ممکن است موجب مشکلات متعددی در تحلیل شود. یکی از مشکلاتی که از وجود هم خطّی چندگانه ناشی می­ شود آن است که مقادیر ضرایب رگرسیون متغیرهای مستقل که همبستگی بالایی دارند تحریف می­ شود. اغلب، این ضرایب تا حدودی پایین هستند و حتی ممکن است از نظر آماری معنی ­دار هم نباشند. دومین مشکل آن است که خطاهای استاندارد وزن­ های رگرسیون متغیرهای پیش ­بین که هم­ خطّی چندگانه دارند ممکن است متورم شود که در نتیجه فواصل اطمینان آن­ها بزرگ خواهد شد، تا جایی که بعضی وقت ­ها این فواصل اطمینان، صفر را نیز در بر می­ گیرد. اگر چنین باشد به یقین نمی­ توان گفت که افزایش اندازه متغیر پیش ­بین موجب افزایش یا کاهش متغیر ملاک می­ شود. مشکل سوم آن است که اگر هم ­خطّی چندگانه به اندازه کافی زیاد باشد عملیات ریاضی درونی خاص (مانند معکوس­ کردن ماتریس) مختل شده و برنامه آماری با سوت­ کشیدن متوقف می­ شود (میزر و دیگران، 237:1391).

دلایل بروز هم­ خطّی چندگانه
یک علّت رایج هم­ خطّی چندگانه این است که پژوهش­گران هم خرده­ مقیاس ­های یک پرسشنامه و هم نمره کل پرسشنامه را به عنوان متغیرهای پیش­بین به ­کار می ­برند. بسته به این که خرده ­مقیاس ­ها چگونه محاسبه شده باشند، این امکان وجود دارد که ترکیب آن­ ها با نمره کل پرسشنامه دارای همبستگی تقریبا کامل باشد. بنابراین باید فقط خرده­ مقیاس ­ها یا نمره کل را پرسشنامه را به­ کار ببریم نه این که همه آن­ها را با هم وارد تحلیل کنیم. علّت رایج دیگر هم­ خطّی چندگانه این است که متغیرهایی در تحلیل وجود دارند که سازه مشابه را می­ سنجند. ما باید همه این متغیرها به جز یک متغیر را از تحلیل کنار بگذاریم، یا احتمال ترکیب آن­ها را با یک روش معقول و منطقی مدنظر قرار بدهیم.

تشخیص هم­ خطّی­ چندگانه
زمانی که فقط دو متغیر بررسی می ­شوند، پیدا کردن رابطه هم ­خطّی از طریق وجود همبستگی بالا آسان است. فقط کافی است که همبستگی­ های پیرسون بین متغیرهای موجود در تحلیل را به عنوان پیش ­درآمد (پیش ­شرط) آزمون ­هایی مانند رگرسیون چندگانه بررسی کنیم. وقتی رابطه بین دو متغیر بسیار قوی است پرچم قرمز برافراشته می ­شود. به عنوان یک قاعده کلی سرانگشتی پیشنهاد می­ کنیم زمانی که همبستگی بین دو متغیر 0/7 یا بالاتر است احتمالا نباید آن­ها را در رگرسیون یا هر ­تحلیل چندمتغیری دیگری با هم به­ کار برد. اگر همبستگی بالاتر از 0/8 باشد، تقریبا بدون شک مشکل خواهیم داشت، اما با مقادیر کمتر از این مقدار هم ممکن است دشواری­ هایی وجود داشته باشد (میزر و دیگران، 1391: 238).
زمانی که بیشتر از دو متغیر بررسی می­ شوند از پارامتر تحمل استفاده می­ کنیم. این پارامتر موجب می­ شود با بیرون­ راندن متغیرهای پیش ­بینی که با سایر متغیرهای مستقل همبستگی بسیار بالایی دارند روش را در برابر خطر هم­خطّی چندگانه حفظ کند. از نظر مفهومی، پارامتر تحمل، مقدار واریانس متغیر پیش­بین است که به وسیله سایر متغیرهای پیش­بین تبیین نشده است (R² بین متغیرهای پیش­بین - 1). دامنه مقادیر پارامتر تحمل از 0 تا 1 است و اندازه ­های پایین ­تر پارامتر تحمل نشان می­ دهد که بین متغیرهای پیش­بین روابط قوی ­تری وجود دارد (میزر و دیگران، 1391:239). اگر اندازه پارامتر تحمل در دامنه 0/4 باشد جای نگرانی دارد، اما اگر در دامنه 0/1 باشد مشکل آفرین است (استیونس،2002). هر چه مقدار پارامتر تحمل به عدد 1 نزدیک ­تر باشد نشان می ­دهد احتمال وجود هم­ خطّی چندگانه کمتر است. لازم به ذکر است که پارامتر تحمل برای تمام متغیرهای پیش­بین ارائه می­ شود و پارامتر تحمل هر متغیر را باید جداگانه ارزیابی کرد.

 
مثال:
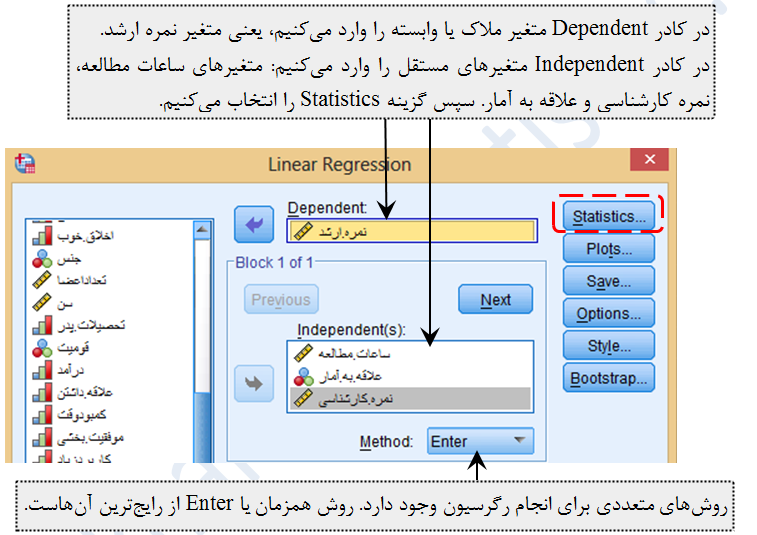
از مثال رگرسیون چند­متغیره برای یافتن هم­ خطّی­ چندگانه استفاده می­ کنیم. متغیرهای مستقل عبارتند از: تعداد ساعات مطالعه، علاقه به درس آمار و نمره درس SPSS در مقطع کارشناسی، متغیر وابسته هم نمره درس SPSS در مقطع ارشد است. در نتیجه ما سه متغیر پیش­بین (مستقل) و یک متغیر ملاک (وابسته) خواهیم داشت. می­ خواهیم بدانیم که آیا بین متغیرهای مستقل هم­خطی چندگانه وجود دارد یا خیر.

جدول 3-3- متغیرهای ملاک و پیش بین

متغیر ملاک	متغیرهای پیش بین
نمره درس SPSS  (ارشد)	ساعات مطالعه علاقه به آمار نمره درس SPSS(کارشناسی)

اگر تنها دو متغیر مستقل وجود داشت از روش همبستگی پیرسون استفاده می­ کردیم و چنانچه ضریب همبستگی بین دو متغیر مستقل بیشتر از 0/7 بود نشان از وجود هم ­خطّی بین متغیرهای مستقل داشت و باید تنها یکی از متغیرهای مستقل را در تحلیل رگرسیون استفاده می­ کردیم. اما در مثال کتاب سه متغیر مستقل داریم و بهتر است از دستور بررسی هم­ خطّی­ چندگانه که در دستور رگرسیون خطّی وجود دارد استفاده کنیم. می­ خواهیم بررسی کنیم که آیا مسأله هم­ خطّی­ چندگانه بین سه متغیر مستقل یا پیش بینِ تعداد ساعات مطالعه، علاقه به درس آمار و نمره درس SPSS (کارشناسی) وجود دارد یا خیر.
 
اجـ ـرا:
مسیر زیر را دنبال می­ کنیم:

Analyze  ---> Regression ---> Linear

 

 
نتـ ـایج:
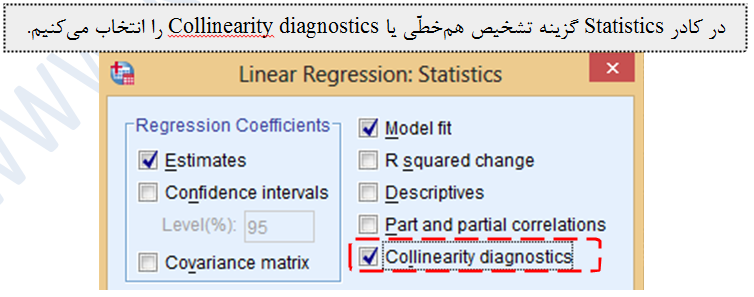
از میان خروجی­ ها و جداول ارائه شده، جدول ضرایب را جهت بررسی هم­ خطّی متغیرهای مستقل بررسی می­ کنیم. در این جدول نتایج ستون آماره تحمّل یا تولرانس نشان دهنده میزان هم ­خطّی متغیرهای مستقل است. 
همان­طور که ذکر شد از نظر مفهومی، پارامتر تحمل، مقدار واریانس متغیر پیش ­بین است که به وسیله سایر متغیرهای پیش ­بین تبیین نشده است. اگر اندازه پارامتر تحمل در دامنه­ ­0/4 باشد جای نگرانی دارد، اما اگر در دامنه 0/1 باشد مشکل ­آفرین است (استیونس، 2002). مطابق نتایج به ­دست­ آمده میزان آماره تحمّل در بین سه متغیر مستقل بیشتر از مقدار 0/4 است و حداقل مقدار آماره تحمّل برابر با 0/63 است. نتایج به ­دست­ آمده نشان­ می ­دهد که میزان هم ­خطّی بین متغیرهای مستقل نگران­ کننده نیست.
آماره تحمّل متغیر نمره کارشناسی 0/632 است که بدین معناست که حدود 63 درصد از واریانس متغیر نمره کارشناسی ارشد توسط دیگر متغیرهای مستقل (ساعات مطالعه و علاقه آمار) تبیین نشده است. چنانچه میزان آماره تحمّل متغیری حدود 0/4 یا کمتر باشد باید اقدام به بازنگری این متغیر کرده و یا آن را از تحلیل حذف کرده و یا اقدام به ترکیب این متغیر با متغیرهایی که دارای ارتباط با آن­ هاست، نمود. 

                                                                                

 

 

 

  

  

  

  

  

 

 

  

  

  

 

 

  

  

  

  

  

  

  

 

 

  

  

  

  

  

  

 

 

  

  

  

  

  

  

 

 

  

  

  

  

  

  

                                                                                                                                                                            

Coefficientsa
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.	Collinearity Statistics
		B ضریب غیراستاندارد	Std. Error خطای استاندارد	Beta ضریب استانداردشده			Tolerance آماره تحمّل
1	(Constant)	13/166	1/369		9/620	0/000
	ساعات مطالعه	0/352	0/049	0/633	7/115	0/000	0/638
	علاقه به آمار	1/512	0/318	0/343	4/750	0/000	0/969
	نمره کارشناسی	-0/029	0/092	-0/028	-/312	0/756	0/632